Public key cryptography is a fundamental technology that secures our digital world. It allows us to send private messages over the internet, verify identities, and protect sensitive data. But how does it work? At its core, public key cryptography relies on mathematical concepts that are both fascinating and essential for modern security. This article will explain these concepts in simple terms, making them accessible to everyone.
What Is Public Key Cryptography?
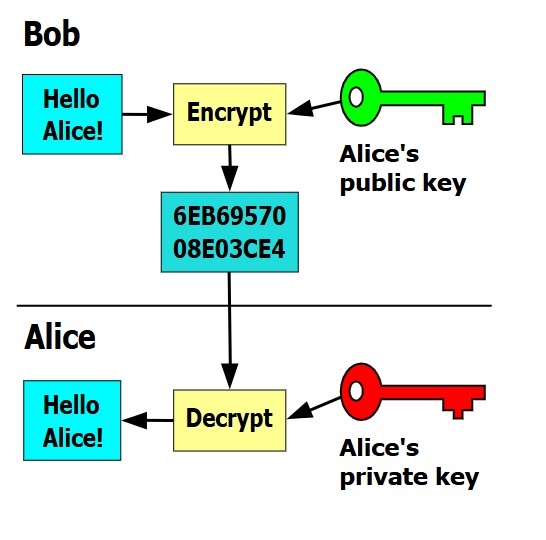
Imagine you want to send a secret message to a friend. You could write it down and hand it to them directly, but what if you're far apart? Traditionally, people would use a shared secret key to encrypt and decrypt messages. However, public key cryptography introduced a revolutionary idea: you can have two keys-one public and one private.
- Public Key: This key is shared openly and can be used by anyone to encrypt a message.
- Private Key: This key is kept secret and is used to decrypt messages that were encrypted with the corresponding public key.
The beauty of this system is that even if someone knows your public key, they cannot decrypt your messages without your private key. This solves the problem of securely sharing secret keys over insecure channels.
The Mathematical Foundations
Public key cryptography relies on certain mathematical problems that are easy to perform in one direction but hard to reverse. These problems form the backbone of its security.
1. The Integer Factorization Problem
One of the earliest and most well-known public key systems is RSA. The security of RSA is based on the difficulty of factoring large composite numbers into their prime factors. While multiplying two large primes is straightforward, factoring their product back into primes is computationally challenging. This asymmetry forms the basis of RSA's security.
2. The Discrete Logarithm Problem
Another foundational problem is the discrete logarithm problem, which underpins systems like Diffie-Hellman and ElGamal. In simple terms, given a number g and another number gx, it's easy to compute gx, but it's hard to determine x without knowing it beforehand. This difficulty ensures the security of these cryptographic systems.
3. The Elliptic Curve Discrete Logarithm Problem
Elliptic Curve Cryptography (ECC) offers a more efficient alternative to traditional systems. ECC uses the mathematics of elliptic curves over finite fields. The discrete logarithm problem in this context is harder to solve than in traditional systems, allowing for shorter key lengths while maintaining strong security.
How Do Public Key Algorithms Work?
Let's explore how some of the most popular public key algorithms function.
RSA Algorithm
RSA works by generating two large prime numbers and multiplying them together to form a modulus. The public key consists of this modulus and an exponent, while the private key is derived from the modulus and the totient of the modulus. (Totient of n is the number of positive integers less than or equal to n that are coprime to n. Two integers are coprime - also called relatively prime or mutually prime - if their greatest common divisor is 1.) Messages are encrypted by raising them to the power of the public exponent modulo the modulus. Decryption is performed using the private key.
Diffie-Hellman Key Exchange
Diffie-Hellman allows two parties to securely share a secret key over an insecure channel. They agree on a large prime number and a base. Each party selects a private key and computes their public key by raising the base to the power of their private key modulo the prime. They exchange public keys and compute the shared secret by raising the received public key to the power of their own private key modulo the prime.
ElGamal Encryption
ElGamal encryption builds on the Diffie-Hellman key exchange. It involves selecting a large prime and a base, then generating a public key by raising the base to the power of a private key modulo the prime. To encrypt a message, a random number is chosen, and the ciphertext (i.e. the encrypted text) consists of two parts: one related to the base raised to the random number and the other related to the message and the public key. Decryption involves using the private key to recover the original message.
Why Is Public Key Cryptography Secure?
The security of public key cryptography relies on the computational difficulty of certain mathematical problems. These problems are easy to perform in one direction but hard to reverse without specific information (like a private key). This asymmetry ensures that even if someone knows the public key, they cannot decrypt messages or forge signatures without the private key.
Real-World Applications
Public key cryptography is used in various applications to secure digital communications:
- Secure Websites (HTTPS): Websites use public key cryptography to establish secure connections with browsers, ensuring that data transmitted between them is encrypted.
- Email Encryption: Email services use public key cryptography to encrypt messages, ensuring that only the intended recipient can read them.
- Digital Signatures: Public key cryptography allows for the creation of digital signatures, which verify the authenticity and integrity of messages or documents.
- Cryptocurrencies: Cryptocurrencies like Bitcoin use public key cryptography to secure transactions and control the creation of new units.
Challenges and Future Directions
While public key cryptography has been a cornerstone of digital security, it faces challenges, especially with the advent of quantum computing. Quantum computers have the potential to solve the mathematical problems underlying current cryptographic systems much faster than classical computers. This has led to research into post-quantum cryptography, which aims to develop new cryptographic systems that are secure against quantum attacks.
Conclusion
Public key cryptography is a powerful and elegant application of mathematics that underpins much of our digital security. By understanding the mathematical principles behind it, we can appreciate how it protects our information and why it's essential for maintaining privacy and trust in the digital age. As technology evolves, so too will the mathematics that keep our communications secure, ensuring that public key cryptography remains a vital tool in safeguarding our digital lives.
You can learn these concepts and more at Dr Hock's maths and physics tuition.